Question

If c is the line segment connecting (x1,y1) to (x2,y2), show that the line integral of xdy-ydx=x1y2-x2y1......this is in a chapter about Green's theorem

Don't answer if you really don't know or understand this kind of stuff. Thanks

Answer 1

Green's theorem doesn't really apply here. GT relates the line integral over some *closed* connected contour that bounds some region (like a circular path that serves as the boundary to a disk). A line segment doesn't form a region since it's completely one-dimensional.

At any rate, we can still compute the line integral just fine. It's just that GT is irrelevant.

We parameterize the line segment by


`\mathbf r(t)=\langle x_1,y_1\rangle(1-t)+\langle x_2,y_2\rangle t`

`\implies\mathbf r(t)=\langle x_1+(x_2-x_1)t,y_1+(y_2-y_1)t\rangle`

with
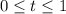
`0\le t\le1`. Then we find the differential:


`\mathbf r(t)\equiv\langle x,y\rangle=\langle x_1+(x_2-x_1)t,y_1+(y_2-y_1)t\rangle`

`\implies\mathrm d\mathbf r\equiv\langle\mathrm dx,\mathrm dy\rangle=\langle x_2-x_1,y_2-y_1\rangle\,\mathrm dt`

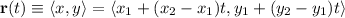
with
`0\le t\le1`.

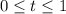
Here, the line integral is


`\displaystyle\int_(\mathcal C)x\,\mathrm dy-y\,\mathrm dx=\int_(\mathcal C)\langle-y,x\rangle\cdot\langle\mathrm dx,\mathrm dy\rangle`

`=\displaystyle\int_(t=0)^(t=1)\langle-y_1-(y_2-y_1)t,x_1+(x_2-x_1)t\rangle\cdot\langle x_2-x_1,y_2-y_1\rangle\,\mathrm dt`

`=\displaystyle\int_(t=0)^(t=1)(x_1y_2-x_2y_1)\,\mathrm dt`

`=(x_1y_2-x_2y_1)\displaystyle\int_(t=0)^(t=1)\,\mathrm dt`

`=x_1y_2-x_2y_1`

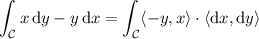
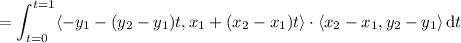
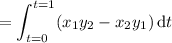
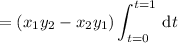
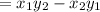
as required.