This problem is about "the rule of three". Notice that the problem is giving us a "ratio", an equivalence between the number of marbles and the dimensions of the rectangular prism. So, the first step would be to find the volume of the rectangular prism.
We know that the volume of a rectangular prism is defined as:
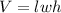
That is, the volume is the product of all three dimensions, which in this case are: 4 inches by 9 inches by 11 inches. So, let's multiplicate
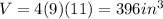
This means 248 marbles fill a 396 cubic inches rectangular prims. That's our initial ratio to apply the rule of three.
Now, we need to find the volume of the new rectangular prims with dimensions 7 inches by 10 inches by 13 inches, that way we'll be able to establish a proportion.
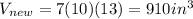
Let's use the rule of three: if 248 marbles fill a 396 cubic inches prism, then how many marbles will fit in a 910 cubic inches prism? (This is the question of our problem) We just need to use a proportion
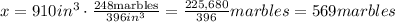
Therefore, in a 910 cubic inches rectangular prism can fit 569 marbles, approximately. It's important to consider that in this case, we can't approximate the number to 570, because we can't fit incomplete marbles.
Notice that the rule of three was applied with the proportions of the problem, the important thing of doing well is that you need to ensure that the result is according to the problem, that is, the question is about marbles, and we got marbles.