Question

Match the following items.

If ∠ADB = 70°, then

1. m∠ABD     = 140
2. m (AB        = 20
3. m (AD        = 40

Answer 1

20, 140, 40 in that order.

Explanation:

Had the question on oddyssey ware.

Answer 2

1. ∠ABD = 20°.

2. Arc AB = 140°.

3. Arc AD = 40°.

Explanation:

Given information: ∠ADB = 70°. BD is diameter.

According to Central angle theorem, the central angle from two chosen points A and B on the circle is always twice the inscribed angle from those two points.

By Central angle theorem,

`\angle DAB=90^(\circ)`

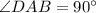
Using angle sum of property in triangle ADB we get,

`\angle ADB+\angle DAB+\angle  ABD=180^(\circ)`

`70^(\circ)+90^(\circ)+\angle  ABD=180^(\circ)`

`\angle  ABD=20^(\circ)`.

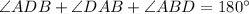
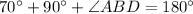
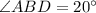Draw a line segment AO.

In triangle AOD, AO=OD, so

`\angle ODB=\angle OAD=70^(\circ)`

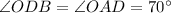
Using angle sum property in triangle AOD,

`\angle AOD+\angle ODA+\angle  OAD=180^(\circ)`

`\angle AOD+70^(\circ)+70^(\circ)=180^(\circ)`

`\angle AOD=40^(\circ)`

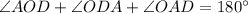
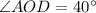
Therefore length of arc AD is 40°.

The angle AOD and AOB are supplementary angles.

`\angle AOD+\angle AOB=180^(\circ)`

`40^(\circ)+\angle AOB=180^(\circ)`

`\angle AOB=140^(\circ)`

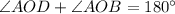
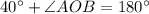
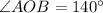
Therefore length of arc AB is 140°.