Question

When two carts having the same mass and the same speed collide and bounce off of each other elastically, what is the final momentum of the carts?

Answer 1

After the collision, the momentum of each cart has the same magnitude as it had before the collision, but in the opposite direction.

Answer 2

The final momentum of the carts (as a system of two masses isolated) is zero.

Step-by-step explanation:

The problem states that two carts with the same mass, and the same speed (in magnitude), collide and bounce off of each other elasticaly. As both carts have the same speed magnitude, in order to collide, they have to be advancing from opposite directions, and in the same line, otherwise they couldn't collide at all.

With this conclusion, we can put the analysis in only one dimension, let's say that they are on a x-axis, they have the same mass, and they have opposite velocity with the same magnitude, before they collide.

The momentum can be written in general as

`p=\sum_(n) m_(n)v_(n)`

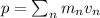
and in our case, n=1, 2.

Then, we calculate the initial momentum in the x-axis, as

`p_(xi)=mv-mv=0`

Therefore, as the initial momentum is zero, and there are no external forces on the system of two masses (weight and normal cancel each other), and they bounce elastically, then the final momentum is equal to the initial momentum, wich means that

`0=-mv+mv=p_(xf)`

So, the final momentum of the carts (as a system of two masses isolated) is zero (wich is equal to the inital momentum).