Question

The table contains a hospital's probability distribution chart of the number of babies born per day for a week. Determine the missing probability inthe distribution, and then answer this question: What percentage of time should a sufficient number of nurses be on duty to care for at least sevenbabies? (Answer to the nearest tenth of a percent.)babies/daY

Answer 1

The percentage of time required is 62.5%

From the probability density function table ;

P(11 - 14) = x

We can find the value of x thus ;

0.125 + 0.25 + 0.4375 + x + 0 = 1

x + 0.8125 = 1

x = 1 - 0.8125

x = 0.1875

The probability of having 7 babies ;

P(>= 7) = P(7 - 10) + P(11 - 14) + P(15 - 20)

P(>= 7) = 0.4375 + 0.1875 + 0

P(>= 7) =0.625

Expressing as a percentage;

0.625 × 100% = 62.5%

Answer 2

Recall that the sum of all probabilities should up to 1. Let x be the probability of 11-14 babies/day.

Then we have the equation

`0.125+0.25+0.4375\text{ + x + 0 = 1}`

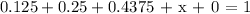
which is equivalent to the equation

`x+0.8125\text{ = 1}`

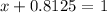
So by subtracting 0.8125 on both sides we get

`x\text{ = 1-0.8125 = 0.1875}`

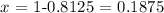
So the probability of having 11-14 babies/day is 0.1875.

Now, to calculate the probability having at least 7 babies, we simply add the probabilities of the events where we have more than 7 babies. That is, sum 7-10 and 11-14 probabilities, which is

`0.4375+0.1875\text{ = 0.625}`

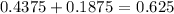
which is close to 63% of the time