Question

I need help because im not sure whether to square it or not
`2 √(n) = n - 3`

Answer 1

To solve the expression:

`2\cdot\sqrt[]{n}=n-3`

We need to square to both sides of the equation. Then, we have:

`(2\cdot\sqrt[]{n})^2=(n-3)^2\Rightarrow4\cdot n=(n-3)^2\Rightarrow4n=n^2-6n+9_{}`

Then,

`n^2-6n+9-4n=0\Rightarrow n^2-10n+9=0`

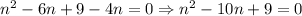
Then, we have that the solutions for this quadratic equation are: n = 1, and n = 9, since

`(n-1)\cdot(n-9)=0,n=1,n=9`

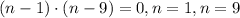
And

`(n-1)\cdot(n-9)=n^2-10n+9`

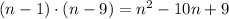
We need to check the results. For n = 1:

`2\sqrt[]{1}=1-3\Rightarrow2\cdot1=-2\Rightarrow2\\e-2`

Then, for n = 1, it is not a solution.

We need to check for n = 9:

`2\cdot\sqrt[]{9}=9-3\Rightarrow2\cdot3=6\Rightarrow6=6`

Then, the solution for the expression above 2*sqrt(n) = n - 3 is n = 9.