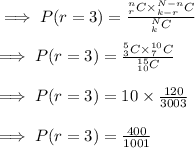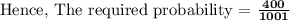Question

A jar of alphabet tiles contains 10 unique consonant tiles and 5 unique vowel tiles.

If 5 tiles are picked randomly, the probability that 3 are consonants and 2 are vowels is
.

Answer 1

Answer: Probability that 3 are consonants and 2 are vowels is 0.3996.

Explanation:

Since we have given that

Number of unique consonant tiles = 10

Number of unique vowel tiles = 5

Total number of tiles = 10+5=15

we need to pick 5 tiles randomly,

So, Probability that 3 are consonants and 2 are vowels is given by

`(^(10)C_3* ^5C_2)/(^(15)C_5)\\\\=((10* 9* 8)/(3* 2* 1)* (5* 4)/(2* 1))/((15* 14* 13* 12* 11)/(5* 4* 4* 3* 2* 1))\\\\=0.3996`

Hence, Probability that 3 are consonants and 2 are vowels is 0.3996.

Answer 2

`\bf\text{The required probability = }(400)/(1001)`

Explanation:

This problem can easily be solved by using Hyper geometric Distribution :

Total number of tiles, N = 15

Number of tiles picked, n = 5

Number of successes, initially , k = 10

Number of successes for which to find, r = 3

Now, we need to calculate P(r = 3)

`\implies P(r = 3)=(_r^n\txterm C * _(k-r)^(N-n)\txterm C)/(_k^N\txterm C)\\\\ \implies P(r=3)=(_3^5\txterm C * _(7)^(10)\txterm C)/(_(10)^(15)\txterm C)\\\\ \implies P(r=3)=10*(120)/(3003)\\\\\implies P(r=3)=(400)/(1001)`

`\bf\text{Hence, The required probability = }(400)/(1001)`