Answer:
C and D
Explanation:
We have to find pairs of functions which are inverses of each other.
1.
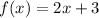 and
and
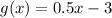
Suppose y=f(x)
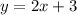
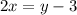
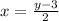
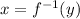
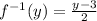
y replace by x
Then , we get

Hence, f(x) and g(x) are not inverses to each other.
B.
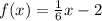 , and
, and
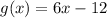
Suppose,
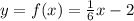

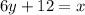
Therefore,
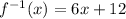
Hence, f(x) and g(x) are not inverses to each other.
C.
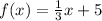 and
and
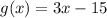
Suppose ,



Therefore,

Hence, f(x) and g(x) are inverses of each other.
D.
 and
and
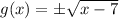
Suppose ,
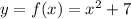

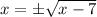
Therefore,
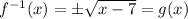
Hence, f(x) and g(x) are inverses to each other.