Question

A photographer needs a frame for an 8 x 10 inch picture, such that the total area is 168 in2. Calculate the width of the frame.

Answer 1

The situation is like this:

The frame has a constant width of x inches, the total area with the frame is 168 in^2

Then, the height of the frame is:

`x+8in+x=2x+8in`

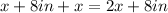
And the length is:

`x+10in+x=2x+10in`

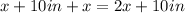
Now, the formula for the area of a rectangle is:

`\text{Area}=height\cdot\text{length}`

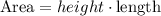
Thus:

`168in^2=(2x+8in)(2x+10in)`

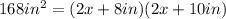
Now, we can solve for x. First, let's apply distributive property:

`168in^2=4x^2+x20in^{}+x16in+80in^2`

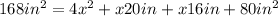
Simplify:

`168in^2=4x^2+x36in+80in^2`

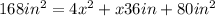
Now, we have a quadratic equation. If one of the sides of the euqal sign is 0, then we can apply the quadratic formula.

The quadratic formula is:

`\begin{gathered} \text{Given }ax^2+bx+c=0 \\ \text{Then:} \\ x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a} \end{gathered}`

THen, if we substract 168in^2 on both sides, we get:

`0=4x^2+x36in+80in^2-168in^2`

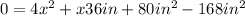
Simplyfied:

`0=4x^2+x36in-88in^2`

Now we can use the quadratic formula:

`x_(1,2)=\frac{-36\pm\sqrt[]{36^2-4\cdot4\cdot(-88)}}{2\cdot4}=\frac{-36\pm\sqrt[]{1296+1408^{}}}{8}=\frac{-36\pm\sqrt[]{2704^{}}}{8}=\frac{-36\pm52^{}}{8}`

The two answers are:

`\begin{gathered} x_1=(-36+52)/(8)=(16)/(8)=2 \\ x_2=(-36-52)/(8)=(-88)/(8)=-11 \end{gathered}`

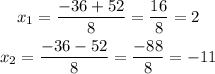
Since one of the solutions is negative, we can rule it out (a negative length doesn't makes sense, thus we stick to the possitive value)

Then, the width of the frame is 2in