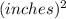Answer:
The area is 9 inches squared
Explanation:
The area of a rectangle is the multiplication of the lenght and the width
Let A be the area, L the lenght and W the width
A = LW
The given lenght is
![\sqrt[3]{81}](https://img.qammunity.org/2018/formulas/mathematics/high-school/40sy4yy9nv8cok4c3orbadkw3j0tdsm0uk.png) inches and the given width is
inches and the given width is
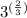 inches
inches
But using a property of exponentials you can rewrite the width as:
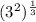
There is another property of exponentials which says that:
![n^{(1)/(k) } = \sqrt[k]{n}](https://img.qammunity.org/2018/formulas/mathematics/high-school/6zon3tn5k1yrkm9u2je9zwqjhrxucuql67.png)
So, the width can be written as:
![\sqrt[3]{3^(2) }](https://img.qammunity.org/2018/formulas/mathematics/high-school/gav51bsoj3h2bbt0k5hbq3583nna6kvwp2.png)
Calculating the area:
![A=\sqrt[3]{81}(\sqrt[3]{9})](https://img.qammunity.org/2018/formulas/mathematics/high-school/ls0uy8wrgfksdbkbup6wcbhg7b96a9j6ah.png)
The multiplication of two cube roots is the cube root of the multiplication of the two numbers
Therefore:
![A=\sqrt[3]{(81)(9)} = \sqrt[3]{729}](https://img.qammunity.org/2018/formulas/mathematics/high-school/hukjrrccdl7f3g4azexi5ehsypx4n3ch4h.png)
A = 9