Question

Pls help me do Calc corrections!

Answer 1

1.
`a=2,b=3` makes it so that


`\displaystyle\lim_(x\to1^-)f(x)=\lim_(x\to1)(3-x)=2`

`\displaystyle\lim_(x\to1^+)f(x)=\lim_(x\to1)(2x^2+3x)=5`

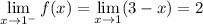
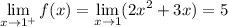
and because the one-sided limits do not agree,
`f(x)` is not continuous at
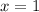
`x=1` under these conditions.

2. For
`f(x)` to be continuous, we need both limits to match up; specifically, we require


`\displaystyle\lim_(x\to1)(ax^2+bx)=a+b=2`

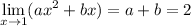
3. Similar to (2), we need the limits from either side of
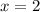
`x=2` to agree:


`\displaystyle\lim_(x\to2^+)f(x)=\lim_(x\to2)(5x-10)=0`

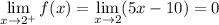
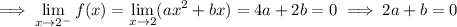
`\implies\displaystyle\lim_(x\to2^-)f(x)=\lim_(x\to2)(ax^2+bx)=4a+2b=0\implies 2a+b=0`

4.
`f(x)` will be continuous everywhere so long as
`a,b` are chosen such that both
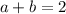
`a+b=2` and
`2a+b=0`.


`a+b=2\implies b=2-a\implies 2a+(2-a)=a+2=0\implies a=-2\implies b=4`

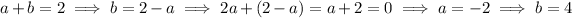
5. I'll leave this part to you.