Question

Use stoke's theorem to evaluate∬m(∇×f)⋅ds where m is the hemisphere x^2+y^2+z^2=9, x≥0, with the normal in the direction of the positive x direction, and f=⟨x^5,0,y^1⟩. begin by writing down the "standard" parametrization of ∂m as a function of the angle θ (denoted by "t" in your answer)

Answer 1

By Stokes' theorem,


`\displaystyle\int_(\partial\mathcal M)\mathbf f\cdot\mathrm d\mathbf r=\iint_(\mathcal M)\\abla*\mathbf f\cdot\mathrm d\mathbf S`

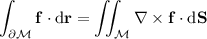
where
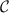
`\mathcal C` is the circular boundary of the hemisphere
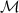
`\mathcal M` in the
`y`-
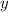
`z` plane. We can parameterize the boundary via the "standard" choice of polar coordinates, setting


`\mathbf r(t)=\langle 0,3\cos t,3\sin t\rangle`

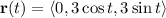
where
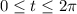
`0\le t\le2\pi`. Then the line integral is


`\displaystyle\int_(\mathcal C)\mathbf f\cdot\mathrm d\mathbf r=\int_(t=0)^(t=2\pi)\mathbf f(x(t),y(t),z(t))\cdot(\mathrm d)/(\mathrm dt)\langle x(t),y(t),z(t)\rangle\,\mathrm dt`

`=\displaystyle\int_0^(2\pi)\langle0,0,3\cos t\rangle\cdot\langle0,-3\sin t,3\cos t\rangle\,\mathrm dt=9\int_0^(2\pi)\cos^2t\,\mathrm dt=9\pi`

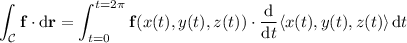
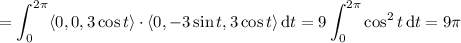
We can check this result by evaluating the equivalent surface integral. We have


`\\abla*\mathbf f=\langle1,0,0\rangle`

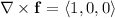
and we can parameterize
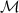
`\mathcal M` by


`\mathbf s(u,v)=\langle3\cos v,3\cos u\sin v,3\sin u\sin v\rangle`

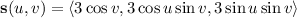
so that


`\mathrm d\mathbf S=(\mathbf s_v*\mathbf s_u)\,\mathrm du\,\mathrm dv=\langle9\cos v\sin v,9\cos u\sin^2v,9\sin u\sin^2v\rangle\,\mathrm du\,\mathrm dv`

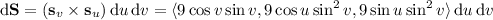
where
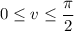
`0\le v\le\frac\pi2` and
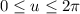
`0\le u\le2\pi`. Then,


`\displaystyle\iint_(\mathcal M)\\abla*\mathbf f\cdot\mathrm d\mathbf S=\int_(v=0)^(v=\pi/2)\int_(u=0)^(u=2\pi)9\cos v\sin v\,\mathrm du\,\mathrm dv=9\pi`

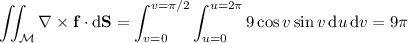
as expected.