Question

Solve the following system of equations by graphing. Then determine whether the system is consistent or inconsistent and whether theequations are dependent or independent. If the system is consistent, give the solution.y = 3x + 36x – 2y = 3

Answer 1

Step-by-step explanation

`\begin{gathered} y=3x+3 \\ 6x-2y=3 \end{gathered}`

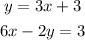
A linear or nonlinear system of equations is called consistent if there is at least one set of values for the unknowns that satisfy each equation in the system—that is, when substituted into each of the equations, they make each equation hold true as an identity.

Therefore, if we substitute equation 1 into equation two we will have;

`\begin{gathered} 6x-2(3x+3)=3 \\ 6x-6x-6=3 \\ -6=3 \end{gathered}`

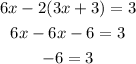
Answer:

Since the result does not give at least one solution to the system of equations, it implies that the system of equations is inconsistent.

The system is also neither dependent nor independent as there are no solutions.