Answer:
Time when the height is 4 feet is given by
 sec or
sec or
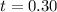 sec
sec
and time taken to reach the ground is 1.125 sec
Explanation:
It is given that the height is given by
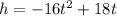
now we need to find the time t when height h= 4 feet , so we plug h= 4 and solve for t, so we have
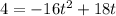
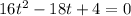 (adding
(adding
 and subtracting
and subtracting
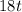 to both sides)
to both sides)
now we can use quadratic formula

we compare
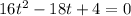 with
with
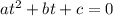
we have
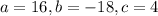
Now we have
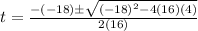
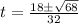

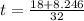 or
or

so the time when the height is 4 feet is given by
 sec or
sec or
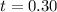 sec
sec
Now height is 0 on the ground, so we plug h=0 to find t
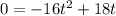
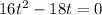 ( we bring all the terms to left side)
( we bring all the terms to left side)
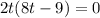
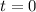 or
or
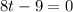 ( we equate each factor to 0)
( we equate each factor to 0)
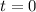 or
or
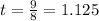
t=0 is the initial time
hence time taken to reach the ground is 1.125 sec