Question

I need to find two consecutive positive integers such that the square of the first is decreased by 17 equals to 4 times the second

Answer 1

so, is two integers, and they must be consecutive, meaning, the next one will have to be either 1 before the first or one after... anyhow.

let's say the first integer is "a".

then a consecutive integer to that one will be just 1 hop away, or say "a + 1", so there, those are the two integers.

now, we know that


`\bf \stackrel{\textit{square of the first is decreased by 17}}{a^2-17}~~=~~\stackrel{\textit{4 times the second}}{4(a+1)} \\\\\\ a^2-17=4a+4\implies a^2-4a-21=0\implies (a-7)(a+3)=0 \\\\\\ a= \begin{cases} \boxed{7}\\ -3 \end{cases}`

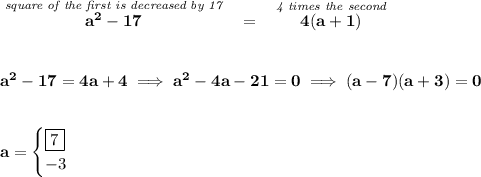
so, is a positive integer, so it can't be -3.

what's the second integer? well is a + 1.