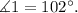Recall that with parallel lines, the following angles are congruent:
Now, two angles are called alternate exterior angles if they are on opposite sides of the transversal line in different lines as shown on the following diagram:
the colors indicate the alternate exterior angles pairs.
Answer:
Since the vertical lines are parallel, then by the alternate exterior angles theorem we know that:
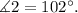
Now, angles 2 and 3 are supplementary, which means that they add up to 180 degrees:
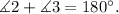
Substituting ∡2=102 degrees and solving for ∡3 we get:
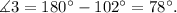
Finally, the angle given and angle 1 are alternate interior angles, therefore: