Answer:
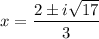
Explanation:
A complex number is the sum of a real number and an imaginary number.
An imaginary number is a non-zero real number multiplied by the imaginary unit
 .
.

For example:
- 5
 is an imaginary number (and its square is -25)
is an imaginary number (and its square is -25) - 5 + 5
 is a complex number
is a complex number
Quadratic Formula
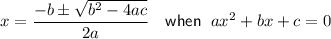
Given quadratic equation:
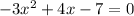
Therefore:
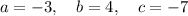
Inputting these values into the quadratic formula:
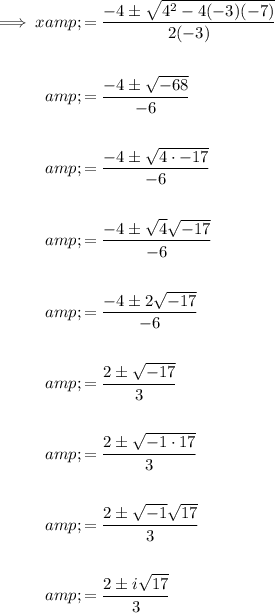
Therefore, the solutions to the given quadratic equation are complex numbers as they include the imaginary number
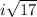 .
.