Question

The monthly sale (in thousands of units) for the t^th month after the introduction of a product in the market is given by S = 135t/(t^2 + 50). In which earliest month would the sale (S) have been 9?

Answer 1

Given the following equation:

`\text{ S = }\frac{135t}{t^2\text{ + 50}}`

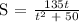
Let's determine t at S = 9.

We get,

`\text{ 9 = }\frac{135t}{t^2\text{ + 50}}`
`(9(t^2+50\rparen)/(9)\text{= }(135t)/(9)`
`\text{ t}^2\text{ + 50 = 15t}`
`\text{ t}^2\text{ -15t + 50}`

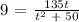
a = 1, b = -15 and c = 50

Apply the quadratic formula:

`\text{ t = x = }\frac{-\text{b }\pm\text{ }\sqrt{\text{b}^2\text{ - 4ac}}}{\text{ 2a}}`
`\text{ = }\frac{\text{ -\lparen-15\rparen }\pm\text{ }\sqrt{(-15)^2\text{ - 4\lparen1\rparen\lparen50\rparen }}}{\text{ 2\lparen1\rparen}}`
`=\text{ }\frac{\text{ 15 }\pm\text{ }\sqrt{\text{ 225 - 200}}}{\text{ 2}}`
`\text{ = }\frac{\text{ 15 }\pm\text{ }\sqrt{\text{25}}}{\text{ 2}}`
`\text{ = }\frac{\text{ 15 }\pm\text{ 5}}{\text{ 2}}`
`\text{ x}_1\text{ = }\frac{\text{ 15 + 5}}{\text{ 2}}\text{ = }(20)/(2)\text{ = 10th month}`
`\text{ x}_2\text{ = }\frac{\text{ 15 - 5}}{\text{ 2}}\text{ = }\frac{\text{ 10}}{\text{ 2}}\text{ = 5th month}`

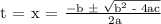
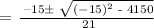
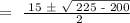
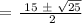
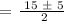
Therefore, the earliest month will be either the 5th or 10th month.

Among the given choices, only the 10th month is in the choices.

Therefore, the answer is CHOICE B : 10th