Given the following equation:
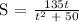
Let's determine t at S = 9.
We get,
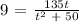
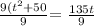
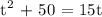
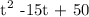
a = 1, b = -15 and c = 50
Apply the quadratic formula:
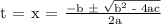
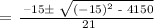
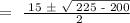
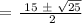
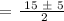
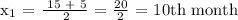
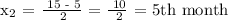
Therefore, the earliest month will be either the 5th or 10th month.
Among the given choices, only the 10th month is in the choices.
Therefore, the answer is CHOICE B : 10th