Question

The table below shows the height of a ball x seconds after being kicked.

What values, rounded to the nearest whole number, complete the quadratic regression equation that models the data?
f(x) = ____ x^2 + _____ x + 0
Based on the regression equation and rounded to the nearest whole number, what is the estimated height after 0.25 seconds?

____ feet

Answer 1

A quadratic regression equation is of the form
y = c₃x² + c₂x +c₁

Coefficients c₁,c₂,c₃ are determined by minimizing the least squared error

`S = \sum _(i=1)^(n) [y_(i) - (c_(3)x_(i)^2+c_(2)x_(i)+c_(1))]^(2)`
This means that

`(\partial S)/(\partial c_(1)) = (\partial S)/(\partial c_(2)) = (\partial S)/(\partial c_(3)) =0`

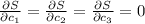
This creates the matrix equation for determining the c-coefficients:

`\begin{bmatrix} n&\sum x&\sum x^(2)\\\sum x&\sum x^(2)&\sum x^(3)\\\sum x^(2)&\sum x^(3)&\sum x^(4) \end{bmatrix} \begin{bmatrix} c_(1)\\c_(2)\\c_(3)\end{bmatrix} = \begin{bmatrix} \sum y\\\sum xy\\ \sum x^(2)y\end{bmatrix}`

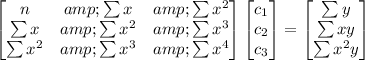
For the given problem,
the matrix equation is

`\begin{bmatrix} 7&10.5&22.75\\10.5&22.75&55.125\\22.75&55.125&142.1875 \end{bmatrix} \begin{bmatrix} c_(1)\\c_(2)\\c_(3)\end{bmatrix} = \begin{bmatrix}475\\935\\2125 \end{bmatrix}`

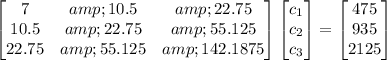
The solution for the coefficients is
c₁ = -0.3571
c₂ = 81.0714
c₃ = -16.4286

The graph of the fitted data is shown below.

When x = 0.25,
y = c₃(0.25)² + c₂(0.25) + c₁ = 18.884

The regression equation is
f(x) = -16.4286x² + 81.0714x - 0.3571
When rounded to the nearest whole number,
f(x) = -16x² + 81x + 0
and
f(0.25) = 19.25

Answers:
f(x) = -16x² + 81x + 0 (approximated)
f(0.25) = 19.25 (approximated)