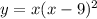Question

End Behavior of Polynomials Functions Identify each characteristic for the graph of the function shown

Answer 1

From the graph

we get that,

Extremum points are (3,-108) and (9,0)

(3,-108) is relative minimum

(9,0) is relative maximum

To describe the function of the given graph

The x intercepts of the function are 0,9

where the curve touches the xa axis at the point x=9

we get the function of the curve as,

`y=(x-0)(x-9)^2`
`y=x(x-9)^2`

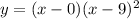
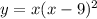
The function of the curves is given by y=x(x-9)^2

Domain of the function is,

`x\in(-\infty,\infty)`

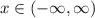
That is x belongs to the whole real line.

Range also belons to the whole real line

To identify the increasing and decreasing intervals,

`\begin{gathered} (+\infty,3)---\text{ decreasing interval} \\ (3,9)-----\text{Increasing interval} \\ (9,-\infty)------\text{ decreasing interval} \end{gathered}`
`\begin{gathered} \text{ as }x\rightarrow\infty\text{ the function is increasing} \\ \text{as }x\rightarrow-\infty\text{ the function is decreasind} \end{gathered}`

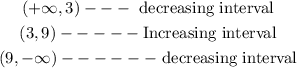
The function of the given graph is,

`y=x(x-9)^2`