HELP NOW PLEASEEEEEEEEEEEE ANSWER NEEDS TO B POSITIVE

Question

asked Oct 6, 2022 5.7k views

2 Answers

Tarun Dholakiya · Answer 1 · 2022-10-08T08:22:30+0000

Answer:

1

Explanation:

So first we do (x^5)^2 which we know is just x^10 because of exponents of powers I believe it's called, basically you just multiply the two powers.

Then you do the bottom half which is x^3 * x^7 and that equals x^10 because of the product of exponent rule,

Then we do x^10/x^10 which = 1 because the same number over the same number is always 1.

Let me know if you have any questions

James In Indy · Answer 2 · 2022-10-13T15:30:28+0000

Answer:

Solving the expression:
((x^5)^2)/((x^7)(x^3)) the answer is 1

Explanation:

We need to solve the expression:
((x^5)^2)/((x^7)(x^3))

We know that exponent rule:
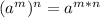
(a^m)^n=a^(m*n)

Applying this rule in numerator

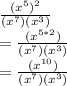
$((x^5)^2)/((x^7)(x^3))\\=((x^(5*2)))/((x^7)(x^3))\\=((x^(10)))/((x^7)(x^3))$

We know the exponent rule:
(a^m).(a^n)=a^(m+n)

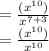
$=((x^(10)))/(x^(7+3))\\=((x^(10)))/(x^(10))$

Now, using the exponent rule:
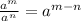
(a^m)/(a^n)=a^(m-n)

$=x^(10-10)\\=x^0$

We know that
a^0=1

So,
x^0=1

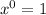
Solving the expression:
((x^5)^2)/((x^7)(x^3)) the answer is 1