Question

What is the volume of a box with width 2 2/3 inches, length 3 1/3 inches, and height 2 1/3 inches ?

Answer 1

The volume of the box is
`20 (20)/(27)` inches

To determine the volume of the box, we have that the formula for calculating volume of a rectangle is expressed as;

V = lwh

Such that;

• V is the volume of the rectangle
• l is the length of the rectangle
• w is the width of the rectangle
• h is the height of the rectangle

Now, substitute the values, we have;

Volume =
`(8)/(3) * (10)/(3) * (7)/(3)`

Multiply the values, we get;

Volume =
`(560)/(27)` inches

Volume is also;

=
`20 (20)/(27)` inches

Answer 2

The volume of a box is:

V = 560 cubic inches or
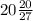`20(20)/(27)` cubic inches.

Explanation:

Given

The width of a box = w = 2 2/3 inches

i.e.
`\:w=2(2)/(3)=(8)/(3)`

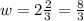
The length of a box = l = 3 1/3 inches

i.e.
`l=\:3(1)/(3)=(10)/(3)`

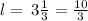
The height of a box = h = 2 1/3 inches

i.e.
`\:h=2(1)/(3)=(7)/(3)`

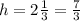
Using the formula to determine the volume of a box

`V=w* l* h`

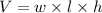
substitute
`\:w=2(2)/(3)=(8)/(3)`,
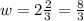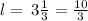`l=\:3(1)/(3)=(10)/(3)` and
`\:h=2(1)/(3)=(7)/(3)`,

`V=(8)/(3)* (10)/(3)* (7)/(3)`

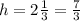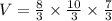
Apply the fraction rule:
`(a)/(b)* (c)/(d)=(a\:* \:c)/(b\:* \:d)`

`=(8* \:10* \:7)/(3* \:3* \:3)`

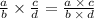
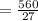`=(560)/(27)` or
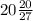`20(20)/(27)` cubic inches

Therefore, the volume of a box is:

V = 560 cubic inches or
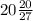`20(20)/(27)` cubic inches.