Question

the density of oxygen is listed in tables as 1.43kgm-³ 'at standard temperature and pressure', meaning 0⁰c and 760mmHg.a) Some oxygen at 20⁰c and under a pressure of 752mmHg occupies a volume of 2.17m³. what volume would it take up 'at standard temperature and pressure'?b)How many kilograms of Oxygen are there in the simple?

Answer 1

ANSWERS

(a) 2 m³

(b) 2.86 kg

Step-by-step explanation

(a) The ideal gas equation is,

`PV=nRT`

Where P is the pressure of the gas, V is the volume it occupies, T is the temperature, n is the number of moles of gas in the sample and R is the universal gas constant.

We want to find the volume of a sample of oxygen if the temperature and pressure are changed. This means that we will have the same number of moles of gas, n and, since R is a constant, the product nR is constant,

`(PV)/(T)=constant`

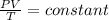
In this case, the initial state of the gas is P₁ = 752 mmHg, V₁ = 2.17 m³, T₁ = 20°C. We have to find the volume V₂ when P₂ = 760 mmHg and T₂ = 0°C. Use the relationship,

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

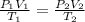
Note that the temperature must be in Kelvin, not degrees Celsius. For that, add 273.15 to each temperature,

`\begin{gathered} \frac{752mmHg\cdot2.17m^3_{}}{(20+273.15)K}=(760mmHg\cdot V_2)/((0+273.15)K) \\ \\ (1631.84)/(293.15)\cdot(mmHg\cdot m^3)/(K)=(760)/(273.15)\cdot(mmHg)/(K)\cdot V_2 \end{gathered}`

Solving for V₂,

`V_2=((1631.84)/(293.15)\cdot(mmHg\cdot m^3)/(K))/((760)/(273.15)\cdot(mmHg)/(K))\approx2m^3`

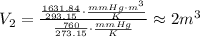
Hence, the volume of the same sample of oxygen at standard temperature and pressure is 2 m³.

(b) To find the mass of oxygen, we have to use the density of that gas,

`\rho=(m)/(V)`

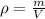
We know that the density ρ = 1.43 kg/m³ and that the volume at standard temperature and pressure is 2m³. Solve the equation above for m,

`m=\rho\cdot V=1.43(kg)/(m^3)\cdot2m^3=2.86kg`

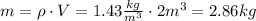
Hence, there are 2.86 kilograms of oxygen in the sample.