Answer:
b = 12 cm
Explanation:
The Pythagora's Theorem
The area of a square of side length x is
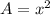
We have three squares, two of which have side lengths of a=5 cm and b= 13 cm.
The combined area of the smaller squares is the same as the area of the largest square. We cannot say at first sight which square is the largest, we'll assume the square of side length of 13 cm is the largest one. Thus:
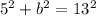
Where b is the unknown side length.
The above expression corresponds to the Pythagora's Theorem formula. Solving for b:
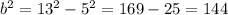
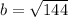
b = 12 cm