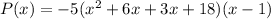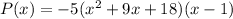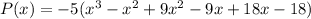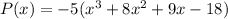Question

The function f(x) is a cubic function and the zeros of f(x) are -6, -3 and 1. The

y-intercept of f(x) is 90. Write the equation of the cubic polynomial in standard
form.

Answer 1

`P(x)=-5x^3-40x^2-45x+90`

Explanation:

Equation of a Polynomial

Given the roots x1, x2, and x3 of a cubic polynomial, the equation can be written as:

`P(x)=a(x-x1)(x-x2)(x-x3)`

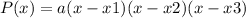
Where a is the leading coefficient.

We know the three roots of the polynomial -6, -3, and 1, thus:

`P(x)=a(x+6)(x+3)(x-1)`

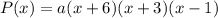
Since the y-intercept of the polynomial is y=90 when x=0:

90=a(0+6)(0+3)(0-1)

90=a(6)(3)(-1)=-18a

Thus

a = 90/(-18) = -5

The polynomial is:

`P(x)=-5(x+6)(x+3)(x-1)`

We must write it in standard form, so we have to multiply all of the factors as follows:

`P(x)=-5(x^2+6x+3x+18)(x-1)`

`P(x)=-5(x^2+9x+18)(x-1)`

`P(x)=-5(x^3-x^2+9x^2-9x+18x-18)`

`P(x)=-5(x^3+8x^2+9x-18)`

`\boxed{P(x)=-5x^3-40x^2-45x+90}`