Answer:
The
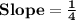
The y-intercept is (0,3)
Option D is correct.
Explanation:
A linear function given has following points:
x y
-8 1
0 3
We need to find slope and y-intercept
To find slope, we can use formula:
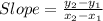
We have x_1=-8, y_1=1, x_2=0, y_2=3
Putting values and finding slope
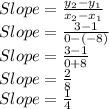
So, we get
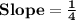
We need to find y-intercept.
y-intercept can be found by putting x =0.
Looking at the table, when x =0, y=3
So, y-intercept is (0,3)
The required answer is:
The
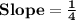
The y-intercept is (0,3)
Option D is correct.