Hello there. To solve this question, we'll have to remember how to use the borda count method.
Given the table with the preferable tables for SGA representatives, we have to determine the rankings and total points for Courtney, Jade and Susan.
We start by remembering the formula:
For this, we multiply the number of votes by the number of choices and add of each person the number of votes multiplied by the position subtracted from n - 1.
For example, let's calculate Susan:
In the first column, she is on the first place and the total votes were 32.
In the second column, she is on the second place and the total votes were 55.
In the third column, she is again on the first place and the total votes were 16.
We have:
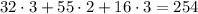
Now, let's calculate Courtney:
Using the same amount of votes, we analyze her positions in the ranking for each column. She was on the second place in the first column, on the first plance in the second and on the third place in the third. This means we get:
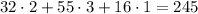
Finally, calculating Jade:
She was on the third place in both first and second columns and on the second place in the third column. This gives us:
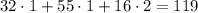
Finally, the winner is given by whoever got the most number of points in the Borda count:
Susan.
The tally is:
==
Does the Borda Count method satisfy the Condorcet criterion in this situation?
Yes, because the Condorcet criterion says whenever we have a Condorcet winner in an election, it'll be choosed as the winner and it means that the winner will be the one that had the majority votes in every head-to-head election against each other of the candidates (Wikipedia)
From this, we know that the number of points in the Borda Count method really shows that the person who gets the most points will be the winner of the election, in this case also the Condorcet winner of the election.