Question

In parallelogram ABCD , diagonals AC¯¯¯¯¯ and BD¯¯¯¯¯ intersect at point E, AE=2x2−3x , and CE=x2+4 . What is AC ?

Answer 1

Refer to the image above.

Now, think about parallelogram properties. What do you know about parallelograms?

Remember that:

1) Opposite sides are congruent and parallel (AB = DC; AD = BC).

2) Opposite angles are congruent (D = B; A = C)

3) Consecutive angles are supplementary (A + D = 180°; A + B = 180°).

4) The diagonals of a parallelogram bisect each other.

Since this problem is dealing with the diagonals of the parallelogram, its important to note this property.

If line segment BD bisects line segment AC, then that means that AC is bisected or split into two congruent segments which is AE and CE in this problem.

If both segments are congruent, then that means that AE = CE. Set the equations equal to each other.

AE = CE

2x² - 3x = x² + 4

Combine like terms by moving them over to their respective sides.

Subtract x² from both sides of the equation.

2x² - 3x - x² = x² - x² + 4

Simplify.

x² - 3x = 4

Move over 4 to the left side of the equation by subtracting it from both sides.

x² - 3x - 4 = 0

Solve the equation using the quadratic formula.

x = -b ± √b² - 4ac / 2a

x = - (-3) ± √(-3)² - 4(1)(-4) / 2(1)

x = 3 ± √9 + 16 / 2

x = 3 ± √25 / 2

x = 3 ± 5 / 2

Divide the solutions into two different equations

x = 3 + 5 / 2 → x = 8 / 2 → x = 4

OR

x = 3 - 5 / 2 → x = -2 / 2 → x = -1

So, your solutions are:

x = 4 and x = -1

You have two solutions, so how can you determine which one is the right one. Well, think about the difference between the two values. One number is positive and the other is negative. In the end, we'll have to reject -1 because we CANNOT have a negative value for a length. So, the answer, ultimately, is that x = 4.

However, we're not done yet because the problem is asking for the length of AC and not just x. So, we have to plug in x with 4 in order to find the total value of AC.


2x² - 3x = x² + 4

2(4)² - 3(4) = (4)² + 4

2(16) - 12 = 16 + 4

32 - 12 = 20

20 = 20

AE = 20 AND CE = 20

By adding both lengths together we get the number 40.

Solution: AC = 40

Answer 2

Given that ABCD is a parallelogram.

And diagonals AC and BD intersect at E point.

Therefore, AE = CE , because the diagonals of a parallelogram bisect each other.

Given AE=2x^2−3x , and CE=x^2+4.

Putting them equal.

`2x^2-3x=x^2+4`

`\mathrm{Subtract\:}4\mathrm{\:from\:both\:sides}`

`2x^2-3x-4=x^2+4-4`

`2x^2-3x-4=x^2`

`\mathrm{Subtract\:}x^2\mathrm{\:from\:both\:sides}`

`2x^2-3x-4-x^2=x^2-x^2`

`x^2-3x-4=0`

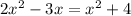
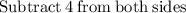
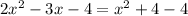
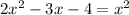
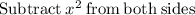
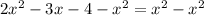
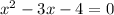
Factoring quadratic

(x-4)(x+1)=0

`x=4,\:x=-1`.

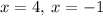We can't take a negative value.

Therefore plugging x=4 in AE=2x^2−3x, we get

AE = 2(4)^2 - 3(4) = 32 - 12 = 20.

AC= 2 × 20 = 40.

Therefore, AC = 40 units.