Answer:
C) ln 5 = 4x is correct option .
Explanation:
Given :
 = 5
= 5
To find : Which logarithmic equation is equivalent to the exponential equation
Solution : We have given that
 = 5.
= 5.
By the exponential form of logarithm:
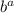 = c then logarithm form is
= c then logarithm form is
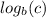 = a.
= a.
Then ,
 = 5 logarithm form is
= 5 logarithm form is
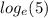 = 4x.
= 4x.
Here,
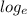 = ln
= ln
So, ln 5 = 4x.
Therefore , C) ln 5 = 4x is correct option .