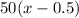Question

A train traveling 50 mph left a station 30 minutes before a second train running at 55 mph. If 55x represents the distance the faster train travels, which of the following algebraic expressions represents the distance of the slower train? 50(x + 0.5) 50(x-0.5) 50(0.5-x)

Answer 1

Equation:
distance = distance
50x = 55(x-(1/2)
50x = 55x - (55/2)
-5x = -55/2
x = 11/2
x = 5 1/2 hrs (time at which the 2nd train overtakes the 1st train)

Answer 2

Option 2nd is correct

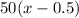`50(x-0.5)` miles

Explanation:

Using distance formula:

`\text{Distance} = \text{Speed} * \text{time}`

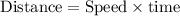
As per the statement:

A train traveling 50 mph left a station 30 minutes before a second train running at 55 mph. If 55x represents the distance the faster train travels.

Second train data:

Let time taken by second train be x hrs

Speed = 55 mph

then;

Distance = 55x miles

First train data:

Speed = 50 mph

time =
`x - (30)/(60) = x - (1)/(2)`

then;

`\text{Distance} = 50(x-(1)/(2))` miles

Since, the second train travels faster than first train

We have to find the distance of the slower train.

Distance of the slower train =
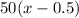`50(x-0.5)` miles

Therefore, the following algebraic expressions represents the distance of the slower train is,
`50(x-0.5)`