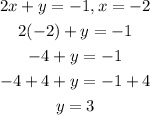Given the two equations below
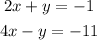
Using the elimination method to solve the the two given equations, we would first ensure that the coefficient of one of the variables in the two equations is the same.
It can be observed that y has the same coefficient for the two equations, so we can eliminate y to x as shown below

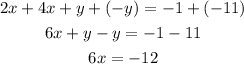
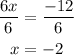
Substitute for x, in equation 1 to find y as shown below