Answer:
We can say that volume of cylinder (452.16) is greater than volume of cone (301.44).
Explanation:
Diameter of cylinder = 8 inches
Diameter of cone = 8 inches
Height of cylinder = 9 inches
Height of cone = 18 inches
We need to find the relationship between the volume of this cylinder and this cone.
First we will find volume of the cylinder
The formula used is:
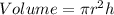
We have
Diameter of cylinder = 8 inches
Radius = d/2 = 8/2 = 4 inches.
Height of cylinder = 9 inches
Putting values and finding volume
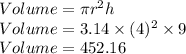
So, Volume of cylinder = 452.16 inches³
Now, we will find volume of the cone
The formula used is:
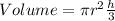
We have
Diameter of cone = 8 inches
Radius = d/2 = 8/2 = 4 inches.
Height of cone = 9 inches
Putting values and finding volume
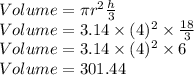
So, Volume of cone = 301.44 inches³
Now, comparing volume of both cylinder and cone.
Volume of cylinder = 452.16 inches³
Volume of cone = 301.44 inches³
We can say that volume of cylinder (452.16) is greater than volume of cone (301.44).