Question

–81, 108, –144, 192, ... Which formula can be used to describe the sequence? f(x) = –81 (4/3) X-1 f(x) = –81 (-3/4) X-1 f(x) = –81 (-4/3) X-1 f(x) = –81 (3/4) X-1

Answer 1

f(x) = –81 (4/3) X-1 f(x) = –81 (-3/4)

Answer 2

Option C.
`f(x)=(-81)(-(4)/(3))^(x-1)`

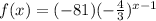
Explanation:

The given sequence is -81, 108, -144, 192,......

We have to get the formula which describes the sequence.

We will get the common factor of this sequence first.

For 1st and second terms

common factor r = -(108)/81 = -12/9 = -4/3

For 2nd and 3rd terms

common factor r = -(144/108) = -16/12 = -4/3

Now we know the explicit formula of an geometric sequence is

`T_(n)=a(r)^(n-1)`

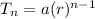
Therefore function which defines the same will be

`f(x)=a(r)^(x-1)`

`f(x)=(-81)(-(4)/(3))^(x-1)`

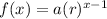
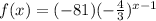
Option C is the correct option.