Question

Determine exactly how many digits the number 2 144,000 has in sexagesimal (base 60) . show all work.

Answer 1

Assuming the number is
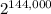
`2^(144,000)`, note that this number requires 144,001 digits in binary. On average, a single digit in base 60 requires about
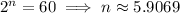
`2^n=60\implies n\approx5.9069` binary digits. But obviously, we have to use a whole number of digits, so we round up to the next integer; in other words, given a number
`x` in base 60 with
`n` digits, we should expect
`x` in base 2 to have
`\lceil5.9069n\rceil`.

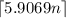
So, if the "conversion rate" from base 60 to base 2 is about 5.9069, then the reverse rate would be
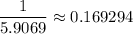
`\frac1{5.9069}\approx0.169294`, i.e. the solution to
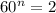
`60^n=2`. Again, we'd have to round up, so if
`x` in base 2 has
`n` digits, then
`x` in base 60 should have
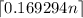
`\lceil0.169294n\rceil` digits.

This means
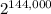
`2^(144,000)` in base 60 would have
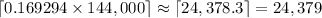
`\lceil0.169294*144,000\rceil\approx\lceil24,378.3\rceil=24,379` digits.