Question

Question 33 of 44A pyramid and a cone are both 12 centimeters tall and have the samevolume. What statement must be true about the two solids?A AA. The area of the cross-sections of the prisms are multiples of eachotherB. The horizontal cross sections of the prisms at the same heightmust have the same areaC. The vertical cross-sections of the prisms at the same width musthave the same areaD. The cross sections of the priams are the same shape

Answer 1

For pyramids shapes like cones and prism pyramids, we can express the volume as one third of the area of the base times the height:

`V=(1)/(3)A_bh`

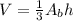
This means that if the cone and the pyramid have the same volume and the same height, they should have the same base area.

If we cross-section the figures at the same height, we won't get the same shape but we should get the same area, as the area of the cross-section will be proportional to the base area, and the base area of both figures are the same.

We can check each statement:

A. They are not multiple of each section. If they are cut at the same height, the cross section of both figures have to have the same area. This statement is false.

B. This statement is true, as both cross section have to have the same area.

C. As the base shapes are different, vertical cross sections may have different areas, so this statement is false.

D. They do not have the same shape but the same area. This statement is false.

Answer: the true statement is Option B.