Answer:
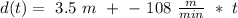
- The whale's depth after 4 min will be 435.5 m.
Explanation:
We want to find the depth d in function of time, for a constant speed, this will take the form
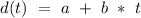 ,
,
we know that at time t = 0 the whale its at 3,5 m below the surface, so we can write:
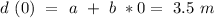
Now, the whale dives at a rate of -1.8 m/s, so the depth increases by 1.8 m/s this must be our b, but before putting it in our equation, we need to convert this to m/min, luckily, we know that one minute has 60 seconds, so :
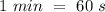 ,
,
dividing for 1 min of each side, we can get our conversion factor:
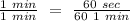
 .
.
Then, we can multiply the whale dives rate for this conversion factor, we are allowed to do that cause the conversion factors equals 1:

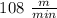
We can put this in our equation for depht:
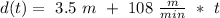
To find what is the depth after 4 min, we just take t = 4 min
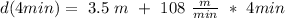 ,
,
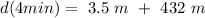 ,
,
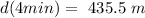 ,
,
So the whale's depth after 4 min will be 435.5 m.