Question

How do I set up 37 and 43

Answer 1

37)

keep in mind that the perimeter of a rectangle is length + length + width + width or P = 2l + 2w, or P = 2(l+w).

we know the perimeter of the box's width and length is 36, therefore then


`\bf \stackrel{P}{36}=2(\stackrel{length}{l}+\stackrel{width}{w})\implies 18=l+w\implies \boxed{18-w=\stackrel{length}{l}} \\\\\\ V(w)=4(w)(18-w)\implies V(w)=-4w^2+72w`

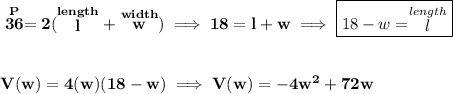
check the first picture below.

now, that parabolic graph, goes up up up reaches a U-turn and the back down, so it has a "maximum" point, and that is when the volume is the highest, namely V(w).


`\bf \textit{ vertex of a vertical parabola, using coefficients}\\\\ \begin{array}{lccclll} V(w) = &{{ -4}}w^2&{{ +72}}w&{{ +0}}\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array}\qquad \left(-\cfrac{{{ b}}}{2{{ a}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right) \\\\\\ {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\implies \stackrel{maximum~volume}{0-\cfrac{72^2}{4(-4)}}`


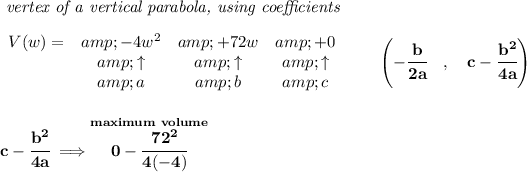
43)

is pretty much the same thing, checking the vertex coordinates of the parabola, check the second picture below,


`\bf h=64t-16t^2\implies h=-16t^2+64t+0\\\\\\ \textit{ vertex of a vertical parabola, using coefficients}\\\\ \begin{array}{lccclll} h = &{{ -16}}t^2&{{ +64}}t&{{ +0}}\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array}\qquad \left(-\cfrac{{{ b}}}{2{{ a}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right) \\\\\\ \stackrel{\textit{it takes this many seconds}}{-\cfrac{64}{2(-16)}}\qquad \qquad \stackrel{\textit{it went up this many feet}}{0-\cfrac{64^2}{4(-16)}}`