Question

The length of a rectangle is one foot more than twice its width if the area of the rectangle is 300 ft^2 find the dimensions of the rectangle

Someone please explain this too me

Answer 1

Width of rectangle = 12 feet

Length of rectangle = 25 feet

Explanation:

We are given the following information in the question:

Let x be the width of the rectangle.

We are given that:

`\text{Length} = 2* \text{Width} + 1\\\text{Length} = 2x +1`

Area of rectangle = 300 square foot

Formula:

`\text{Area of rectangle} = \text{Length}* \text{Width}`

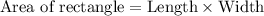
Putting the values, we get,

`300 = x* (2x +1)\\300 =2 x^2 + x\\2x^2 + x -300 = 0`

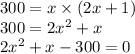
We use the quadratic formula to solve this quadratic equation:

`ax^2 + bx + c = 0\\\\x = \displaystyle(-b\pm √(b^2-4ac))/(2a)`

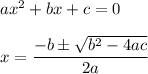
Using the quadratic formula:

`2x^2 + x -300 = 0\\\\x = \displaystyle(-1 \pm √(1+2400))/(4) = \displaystyle(-1 \pm 49)/(4)\\\\x = 12,(-25)/(2)`

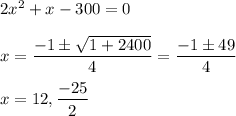
Considering the positive value of x

Width of rectangle = 12 feet

Length of rectangle = 2x + 1 = 25 feet