Question

Use the Intermediate Value Theorem to choose the intervals over which the function, x^4 - 2x^2 - 1, is guaranteed to have a zero. Select all that apply.

a. [-2,-1]
b. [-1,0]
c. [0,1]
d. [1,2]

Answer 1

Let f(x) be the given function.
Answer is a and d, because f(-2)<0 and f(-1)>0; and f(1)<0 and f(2)>0, so there is a change of sign, signifying that between the limits there is a value of x where f(x) must be 0 (the curve crosses the x axis).

Answer 2

Options a. and d. are correct

Explanation:

Intermediate Value Theorem:

Let f be a continuous function on
`\left [ a,b \right ]` such that for a number p,
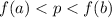`f(a)<p<f(b)` then there exists q in
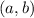`\left ( a,b \right )` such that f(p) = q

Let f(x) =
`x^4 - 2x^2 - 1`

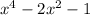
For a. [-2,-1] :

f(-2)=7>0 and f(-1) = -2 < 0 such that f(-1) < 0 < f(-2) then as per the theorem, there exists a number c in (-2,-1) such that f(c) = 0

For d. [1,2]:

f(1)= - 2<0 and f(2) = 7 > 0 such that f(1) < 0 < f(2) then as per the theorem, there exists a number c in (1,2) such that f(c) = 0

So, options a. and d. are correct