Answer:
The solution to the system of equations is (3, 2) and because both lines pass through this point.
Hence, option D is correct.
Explanation:
Given the system of equations
Line A: y = x − 1
Line B: y = −3x + 11
Arrange equation variables for elimination
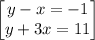
subtracting the equations
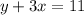

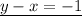
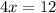
solving 4x = 12 for x
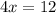
divide both sides by 4

Simplify
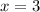
For y = x − 1, substutute x = 3
y = x-1
y = 3 - 1
y = 2
Thus,
(x, y) = (3, 2)
Therefore,
The solution to the system of equations is (3, 2) and because both lines pass through this point.
Hence, option D is correct.