Question

Timothy leaves home for skedunk 400 miles away. after 2 hours, he has to reduce his speed by 20 mph due to rain. if he takes 1 hour for lunch and gas, and reaches skedunk 9 hours after he left home, what was his initial speed?

Answer 1

The entire trip took him 9 hours.
It took him 1 hour for lunch and gas, so he drove for 8 hours.
He drove a total of 400 miles.
He drove the first x miles at a higher speed, s, for 2 hours.
Then he drove the rest of the distance, 400 - x miles, at a lower speed, s - 20, for 6 hours.

speed = distance/time

distance = speed * time

First part of the trip:

x = s * 2

x = 2s

Second part of the trip:

400 - x = (s - 20) * 6

400 - x = 6s - 120

Substitute x = 2s in the equation just above:

400 - 2s = 6s - 120

-8s = -520

s = 65

The initial speed is 65 mph.

Answer 2

65mph.

Explanation:

This problem is divided in two parts. The first part of the travel takes 2 hours and x miles at a unknown speed which we are gonna call
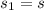`s_(1) =s`. The second part takes 6 hours, because the total hours is 9, but the driver took 1 hour for lunch and gas. Also, during the second part, the driver decreased his speed in 20, so the speed for the second part is
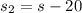`s_(2)=s-20`, and the distance covered is gonna be 400-x because we know that the total distance is 400 miles.

Next, we have to use the equation of a constant movement which involves speed, distance and time.

First part:

`d_(1)=s_(1) t_(1)\\x=s(2hr)=2s`

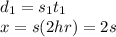
So, the distance covered during the first part is 2s.

Second part:

`d_(2)=s_(2)t_(2)   \\400-x=(s-20)6hr\\400-x=6s-120`

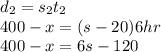
But, we know that
`x=2s`

Then,
`400-x=6s-120\\400-2s=6s-120\\400+120=6s+2s\\520=8s\\s=(520)/(8) =65`

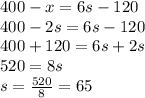
Therefore, the initial speed is
`65mph.`