Question

Working together, merry and pippin can build a wall in 4.5 hours. if merry can do the job alone in 6 hours working alone, how long would it take pippin to build the wall when working alone?

Answer 1

Merry builds 100% wall for 6 hours. For 4.5 hours she did 75% of wall (4.5 * 100 /6) , rest 25% did another girl for 4.5 hours. If she builds wall alone she would spend 18 hours.

Answer 2

ANSWER

`18 \: hours`

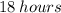
Step-by-step explanation

If Merry and Pippin can build a wall in 4.5 hours, their working rate is


`(1)/(4.5) = (1)/( (9)/(2) ) = (2)/(9)`

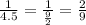
If Merry can do the work alone in 6 hours, then her rate of working is,


`(1)/(6)`

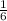
If Pippin takes

`x \: hours`
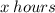
to do the work alone, then her working rate is


`(1)/(x)`

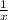
If we add their individual rates it should give us their combined rate.

This means that,


`(1)/(x) + (1)/(6) = (1)/(4.5)`

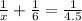
or


`(1)/(x) + (1)/(6) = (2)/(9)`

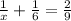
This implies that,


`(1)/(x) = (2)/(9) - (1)/(6)`

We collect LCM on the right hand side to get,


`(1)/(x) = (4 - 3)/(18)`

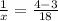
This simplifies to,


`(1)/(x) = (1)/(18)`

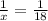
We cross multiply to get,


`18 = x`

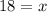
Or


`x = 18`

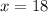
Therefore it would take Pippin, 18 hours to build the wall when working alone.