Question

The length of a rectangle is 2 more than twice the width. find the dimensions of the rectangle if the perimeter is 76. if x represents the width of the rectangle, then which expression represents the perimeter? 2x + 2 4x + 4 6x + 4

Answer 1

The length is 2 more than twice the width L = 2 + 2* x so one equation is L=2+2x the perimeter of a rectangle is found by adding up all the sides so you have x+x+L+L=76 2x+2L=76 ------ if you want to find the dimensions (use the equations i have above) 2x+2(2+2x)=76 2x+4+4x=76 6x+4=76 6x=76-4 6x=72 x=12 is the width so the length is L=2+2x=2+2(12)=2+24=26

Answer 2

• The expression which represents the perimeter is:

`6x+4`

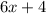
• The length of the rectangle is: 26 units.

• The width of the rectangle is: 12 units.

Explanation:

x represents the width of the rectangle.

Also, the length of a rectangle is 2 more than twice the width.

i.e. the length of the rectangle is given by:

2x+2

Now, we know that the perimeter of the rectangle is given as the sum of all the sides of a rectangle and is given by:

`\text{Perimeter}=2(L+W)`

where L is the length of the rectangle and W is the width of the rectangle.

Hence, here the expression which represents the perimeter is:

`2(3x+2)=6x+4`

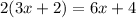
Hence, based on the given question we have:

`2(2x+2+x)=76\\\\2(3x+2)=76\\\\3x+2=(76)/(2)\\\\3x+2=38\\\\3x=38-2\\\\3x=36\\\\x=(36)/(3)\\\\x=12`

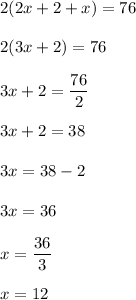
Hence, the width of the rectangle is: 12 units.

and the length of the rectangle is: 2×12+2=26 units.