Question

Consider the following coordinates

W(1,8), X (7,8), Y(4,5), Z(1,2)

Select all methods you could use to prove triangle WYZ is congruent to triangle WYX.

a) Ruler/Protractor
b) Distance formula (SSS)
c) Slope/distance formula (SAS)
d) Transitive property
e) Vertical angles theorem
f) Alternate interior angles theorem
g) Corresponding angles theorem

Answer 1

The methods that could be used to prove triangle WYZ is congruent to triangle WYX are:

a) Ruler/Protractor
b) Distance formula (SSS)
c) Slope/distance formula (SAS)

Answer 2

Answer: a) Ruler/Protractor

b) Distance formula (SSS)

c) Slope/distance formula (SAS)

Explanation:

a) Since, With plotting the points in coordinate plane,

We found the measurement of sides

WX = 6 unit, ZY= 3√2 unit WY = 3√2, WZ = 6 unit and XY = 3√2

Thus, WX ≅ WZ, ZY≅XY and WY≅WY

Therefore By SSS postulate of congruence,

Δ WYZ ≅ Δ WYX

Now, With help of Protector,

We can find the angles ZWY, ZYW, XWY and XYW.

And, we found that, ∠ ZWY≅∠ XWY, and ∠ZYW≅∠XYW

And, WY≅ WY

Therefore, BY ASA postulate of congruence,

Δ WYZ ≅ Δ WYX

b) With help of distance formula,

`WX =√((7-1)^2+(8-8)^2) = 6` unit

`ZY= √((4-1)^2+(5-2)^2) =3√(2)` unit

`WY= √((4-1)^2+(5-8)^2) =3√(2)` unit

`WZ= √((1-1)^2+(2-8)^2) =6` unit

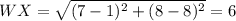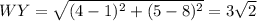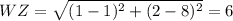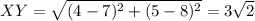`XY= √((4-7)^2+(5-8)^2) =3√(2)` unit

Thus, WX ≅ WZ, ZY≅XY and WY≅WY

Therefore By SSS postulate of congruence,

Δ WYZ ≅ Δ WYX

c) With help of Slope formula we found that,

Slop of the line WX is 0. ( Slope formula
`m=(y_2-y_1)/(x_2-x_1)` )

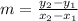And, Slope of line WZ=
`\infty`

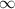
Thus, ∠ZWX=90°

But, ∠YWX=45° ( By the formula of
`tan\theta =(m_1-m_2)/(1+m_1m_2)` )

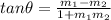⇒∠ZWY=45°

And, By the distance formula, WZ≅WX

∠ZWY≅∠XWY

And, WY≅ WY

Thus, By SAS postulate of congruence,

ΔWYZ≅ΔWYX

Note: with the help of other Options we can not conclude triangle WYZ is congruent to triangle WYX.