Question

Can 3.65909090909 be expressed as a fraction whose denominator is a power of 10? Explain.

Answer 1

`\bf 3.659\textit{ can also be written as }\cfrac{3659}{1000}\textit{ therefore }3.6590909\overline{09}\\\\ \textit{can be written as }\cfrac{3659.0909\overline{09}}{1000}`

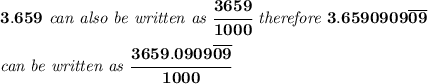
notice above, all we did, was isolate the "recurring part" to the right of the decimal point, so the repeating 09, ended up on the right of it.

now, let's say, "x" is a variable whose value is the recurring part, therefore then


`\bf \cfrac{3659.0909\overline{09}}{1000}\qquad \boxed{x=0.0909\overline{09}} \qquad \cfrac{3659+0.0909\overline{09}}{1000}\implies \cfrac{3659+x}{1000}`

now, the idea behind the recurring part is that, we then, once we have it all to the right of the dot, we multiply it by some power of 10, so that it moves it "once" to the left of it, well, the recurring part is 09, is two digits, so let's multiply it by 100 then,


`\bf \begin{array}{llllllll} 100x&=&09.0909\overline{09}\\ &&9+0.0909\overline{09}\\ &&9+x \end{array}\quad \implies 100x=9+x\implies 99x=9 \\\\\\ x=\cfrac{9}{99}\implies \boxed{x=\cfrac{1}{11}}\\\\ -------------------------------\\\\ \cfrac{3659.0909\overline{09}}{1000}\qquad \boxed{x=0.0909\overline{09}} \quad \cfrac{3659+0.0909\overline{09}}{1000}\implies \cfrac{3659+x}{1000} \\\\\\ \cfrac{3659+(1)/(11)}{1000}`

and you can check that in your calculator.