Question

Using a graph, it can be seen that the curves y=x+ln(x)y=x+ln⁡(x) and y=x3−xy=x3−x intersect at the points (0.447141,−0.357742)(0.447141,−0.357742) and (1.507397,1.917782).(1.507397,1.917782). Find the coordinates (to three decimal places) of the centroid for the region bounded by these curves.

Answer 1

The area of the region bounded by two curves f(x) and g(x) is with poins of intersection at x = a and x = b is given by:


`Area= \int\limits^b_a {\left(f(x)-g(x)\right)} \, dx`

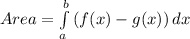
Given the curves
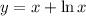
`y=x+\ln x` and
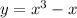
`y=x^3-x`, the area bounded by the curves is given by:


`Area= \int\limits^(1.507397)_(0.447141) {(x+\ln x)-(x^3-x)} \, dx \\ \\ =\int\limits^(1.507397)_(0.447141) {(2x+\ln x-x^3)} \, dx \\ \\ =\left[x^2+x\ln x-x- (1)/(4)x^4 \right]^(1.507397)_(0.447141) \\ \\ =\left[(1.507397)^2+1.507397\ln1.507397-1.507397- (1)/(4) (1.507397)^4\right] \\ -\left[(0.447141)^2+0.447141\ln0.447141-0.447141- (1)/(4) (0.447141)^4\right] \\ \\ =0.092686-(-0.617095)=0.709781\approx\bold{0.710}`

The x-cordinate of the centroid of the area bounded by the two curves is given by:


`C_x= \frac{\int\limits^(1.507397)_(0.447141) {x\left[(x+\ln x)-(x^3-x)\right]} \, dx}{Area} \\ \\ =\frac{\int\limits^(1.507397)_(0.447141) {\left(2x^2+x\ln x-x^4\right)} \, dx}{0.709781} \\ \\ = (\left[ (2)/(3) x^3+ (1)/(2)x^2\ln x- (1)/(4) x^2- (1)/(5) x^5 \right]^(1.507397)_(0.447141))/(0.709781) \\ \\ = (0.625068-(-0.0744211))/(0.709781) \\ \\ = (0.6994891)/(0.709781) \approx0.985`

The y-cordinate of the centroid of the area bounded by the tw.o curves is given by:


`C_y= \frac{\int\limits^(1.507397)_(0.447141) {\left[(x+\ln x)^2-(x^3-x)^2\right]} \, dx}{2(Area)} \\ \\ =\frac{\int\limits^(1.507397)_(0.447141) {\left(2x\ln x+(\ln x)^2-x^6+2x^4\right)} \, dx}{2(0.709781)} \\ \\ = (\left[x^2\ln x- (1)/(2) x^2+x(\ln x)^2-2x\ln x+2x- (1)/(7) x^7+ (2)/(5) x^5 \right]^(1.507397)_(0.447141))/(1.419562) \\ \\ = (2.41459-1.64949)/(1.419562) \\ \\ = (0.7651)/(1.419562) \approx0.539`

Therefore, the coordinates of the centroid of the area bounded by the given two curves is (0.985, 0.539)