Question

The magnitudes and directions of two forces acting at a point P are given in (a) and (b). Approximate the magnitude and direction of the resultant vector. (Round your answers to the nearest whole number.) (a) 70 lb, N75°W (b) 60 lb, S5°E

Answer 1

For vector a:

Horizontal component = -70 cos 15 = -67.613
Vertical component = 70 sin 15 = 18.116

For vector b:

Horizontal component = 60 cos 85 = 5.232
Vertical component = -60 sin 85 = -59.772

For the resultant vector:

Horizontal component = -67.613 + 5.232 = -62.381
Vertical component = 18.116 - 59.772 = -41.656

Magnitude of the resultant vector is given by:


`Magnitude= √((-62.381)^2+(-41.656)^2) \\ \\ = √((3,891.3892+1,735.2223)) = √(5,626.6115) \\ \\ = 75 lb`

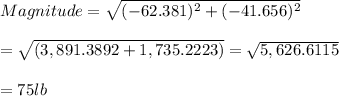
Direction of the resultant vector is given by:


`\tan\theta= (-41.656)/(-62.381) =0.6678 \\ \\ \theta=\tan^(-1)0.6678=214^o`

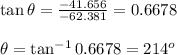
Therefore, the magnitude of the resultant force is 75 lb and the direction of the resultant force is S56°W