Question

B. Write an exponential equation for the world population growth after 2010. Let P = the projected population in billions and t = the number of years after 2010. Hint: Think about how you calculated the entries in the table. If you started with 6.9 billion each time, how could you calculate each population? Think back to your work in the lesson._________C. Use your model to predict the population in 2020._______ Billions

Answer 1

a)

The population in 2011 is that of 2010 plus 1.1% (=0.011) of the population in 2010; therefore

`P_(2011)=P_(2010)+0.011P_(2010)=(1.011)P_(2010)\approx6.98billion`

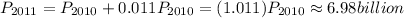
The answer to the first gap is 6.98.

Similarly, in the case of 2012,

`\begin{gathered} P_(2012)=(1.011)P_(2011)=(1.011)^2P_(2010)\approx7.05billion \\ \end{gathered}`

The answers to the second row of gaps are 2 and 7.05 (2 years after 2010 and 7.05billion).

Finally,

`P_(2013)=(1.011)^3P_(2010)\approx7.13billion`

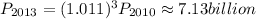
The answers to the third row of gaps are 3 and 7.13

b)

Notice that the pattern below emerges from the table in part a)

`P_(2010+n)=(1.011)^nP_(2010)`

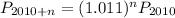
Thus, the exponential equation that models the population is

`\Rightarrow P(t)=6.9*(1.011)^t=6.9(1.011)^t`

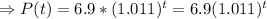
The answer to part b) is 6.9(1.011)^t

c) 2020 occurs 10 years after 2010; therefore, setting t=10 in the equation found in part b)

`P(10)=6.9(1.011)^(10)\approx7.70`

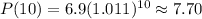
The rounded answer is 7.70