Question

A woman lives on the eighth floor of an apartment building. She works in a high-rise office building 6.5 blocks away from her apartment on the same street. Her office is on the 14th floor. Assume each story of her apartment building is 4.0 m, each story of her office building is 5.5 m, and a block is 146.6 m long.

Required:
a. Sketch her path.
b. Estimate the distance she travels to work.
c. Find the magnitude of her displacement.

Answer 1

b) d = 997.9 m , c) D = (952.9 i ^ +45 k ^) m , D = 953.6 m and θ = 2.7º

Step-by-step explanation:

In this exercise we must add the distance traveled, remembering that the displacement is a vector and the distance a scalar.

a) The displacement scheme is the woman walks in her building A to descend to the lower floor 4.0 m, we assume that this includes the vertical displacement, until reaching the street level, the displacement is vertical in this part.

Being on the street, she travels the 6.5 blocks to reach the building where she works, they indicate that each block is 146.6 m, this movement is horizontal.

Upon reaching building B, she goes up to his office on the 14th floor where she travels 5.5m on each floor, it is assumed that the distance to go up to the upper floor is included, this displacement is vertical

b and c) Let's find the distance traveled and the displacement

in building A

Zₐ = 8 * 4.0

Zₐ = -32.0 m k ^

the vector k ^ indicates that the displacement is vertical and the negative sign that it is descending

on the street

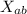`X_(ab)` = 6.5 146.6

X_{ab} = 952.9 m i ^

the vector i ^ indicates that the displacement is the x-axis, we assume that the axis is in the direction of the displacement

in building B

`Z_(b)` = 14 * 5.5

Z_{b} = 77 m k ^

displacement in the vertical axis and in the positive direction

now we calculate the distance traveled,

d = Zₐ + X_{ab} + Z_{b}

d = -32 + 952.9 + 77

d = 997.9 m

note that this value is a scalar

Let's calculate the displacement,

Z axis

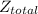`Z_(total)` = Zₐ + Z_{b}

Z_{total} = -32 + 77

Z_{total} = 45 m k ^

X axis

X_{total} = X_{ab}

X_{total} = 952.9 m i ^

we can give the result in two ways

a) D = X_total i ^ + Z_total k ^

D = (952.9 i ^ +45 k ^) m

b) in module form and angles

Let's use the Pythagorean theorem

D² =
`X_(total)^2` +
`Z_(total)^2`

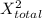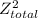
D = √(952.9² + 45²)

D = 953.6 m

We use trigonometry

tan θ = Z / X

θ = tan⁻¹ (Z / X)

θ = tan⁻¹ (45 / 952.9)

θ = 2.7º

this angle is measured from the positive side of the x axis towards the z axis